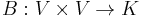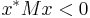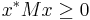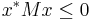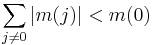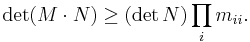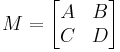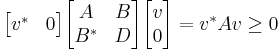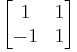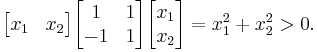Positive-definite matrix
In linear algebra, a positive-definite matrix is a matrix that in many ways is analogous to a positive real number. The notion is closely related to a positive-definite symmetric bilinear form (or a sesquilinear form in the complex case).
The proper definition of positive-definite is unambiguous for Hermitian matrices, but there is no agreement in the literature on how this should be extended for non-Hermitian matrices, if at all. (See the section Non-Hermitian matrices below.)
Contents |
Definition
An n × n real matrix M is positive definite if zTMz > 0 for all non-zero vectors z with real entries (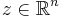 ), where zT denotes the transpose of z.
), where zT denotes the transpose of z.
An n × n complex matrix M is positive definite if ℜ(z*Mz) > 0 for all non-zero complex vectors z, where z* denotes the conjugate transpose of z and ℜ(c) is the real part of a complex number c.
An n × n complex Hermitian matrix M is positive definite if z*Mz > 0 for all non-zero complex vectors z. The quantity z*Mz is always real because M is a Hermitian matrix.
Examples
- The matrix
 is positive definite. For a vector with entries
is positive definite. For a vector with entries 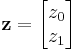 the quadratic form is
the quadratic form is 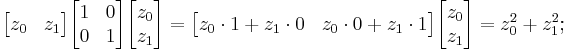
when the entries z0, z1 are real and at least one of them nonzero, this is positive.
- An example of a matrix that is not positive, but is positive-definite, is given by
It is positive definite since for any non-zero vector 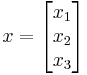 , we have
, we have
which is a sum of squares and therefore nonnegative; in fact, each squared summand can be zero only when 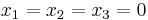 , so
, so 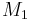 is indeed positive-definite.
is indeed positive-definite.
- Conversely, the strictly positive matrix
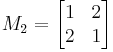 is not positive definite, showing (together with the previous example) that these two properties are independent. Evaluated at
is not positive definite, showing (together with the previous example) that these two properties are independent. Evaluated at 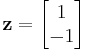 , the quadratic form is
, the quadratic form is 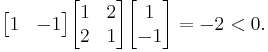
- For a huge class of examples, consider that in statistics positive definite matrices appear as covariance matrices. In fact, every positive definite matrix is the covariance matrix of some multivariate probability distribution.
Characterizations
Let M be an n × n Hermitian matrix. The following properties are equivalent to M being positive definite:
| 1. | All eigenvalues λi of M are positive. Recall that any Hermitian M has an eigendecomposition M = P−1DP where P is a unitary matrix whose rows are orthonormal eigenvectors of M, forming a basis, and D is a diagonal matrix. Therefore M may be regarded as a real diagonal matrix D that has been re-expressed in some new coordinate system. This characterization means that M is positive definite if and only if the diagonal elements of D (the eigenvalues) are all positive. In other words, in the basis consisting of the eigenvectors of M, the action of M is component-wise multiplication with a (fixed) element in Cn with positive entries. |
| 2. | The sesquilinear form
defines an inner product on Cn. (In fact, every inner product on Cn arises in this fashion from a Hermitian positive definite matrix.) In particular, positive definiteness for a Hermitian M is equivalent to the fact that |
| 3. | M is the Gram matrix of some collection of linearly independent vectors
for some k. That is, M satisfies: The vectors xi may optionally be restricted to fall in Cn. In other words, M is of the form |
| 4. | All the following matrices have a positive determinant (Sylvester's criterion):
In other words, all of the leading principal minors are positive. For positive semidefinite matrices, all principal minors have to be non-negative. The leading principal minors alone do not imply positive semidefiniteness, as can be seen from the example |
| 5. | There exists a unique lower triangular matrix  , with strictly positive diagonal elements, that allows the factorization of , with strictly positive diagonal elements, that allows the factorization of  into into
where |
| 6. | The quadratic function associated with M
is, regardless of b, a strictly convex function. |
For real symmetric matrices, these properties can be simplified by replacing 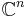 with
with 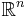 , and "conjugate transpose" with "transpose."
, and "conjugate transpose" with "transpose."
Quadratic forms
Echoing condition 2 above, one can also formulate positive-definiteness in terms of quadratic forms. Let K be the field R or C, and V be a vector space over K. A Hermitian form
is a bilinear map such that B(x, y) is always the complex conjugate of B(y, x). Such a function B is called positive definite if B(x, x) > 0 for every nonzero x in V.
Simultaneous diagonalization
Two symmetric, positive-definite matrices can be simultaneously diagonalized, although not necessarily via a similarity transformation. This result does not extend to the case of three or more matrices. In this section we write for the real case, extension to the complex case is immediate.
Let  and
and  be two positive-definite matrices. Write the generalized eigenvalue equation as
be two positive-definite matrices. Write the generalized eigenvalue equation as 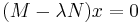 where
where 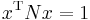 . Now we can decompose the inverse of
. Now we can decompose the inverse of  as
as 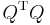 (so
(so  must be positive definite, as the proof shows, in fact it is enough that
must be positive definite, as the proof shows, in fact it is enough that  is symmetric). Now multiply various places with
is symmetric). Now multiply various places with  to get
to get 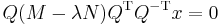 which we can rewrite as
which we can rewrite as 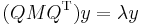 where
where 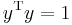 . Manipulation now yields
. Manipulation now yields 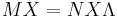 where
where  is a matrix having as columns the generalized eigenvectors and
is a matrix having as columns the generalized eigenvectors and 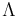 is a diagonal matrix with the generalized eigenvalues. Now premultiplication with
is a diagonal matrix with the generalized eigenvalues. Now premultiplication with 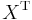 gives the final result:
gives the final result:
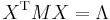 and
and 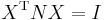 , but note that this is no longer an orthogonal diagonalization.
, but note that this is no longer an orthogonal diagonalization.
Note that this result does not contradict what is said on simultaneous diagonalization in the article Diagonalizable matrix#Simultaneous diagonalisation, which refers to simultaneous diagonalization by a similarity transformation. Our result here is more akin to a simultaneous diagonalization of two quadratic forms, and is useful for optimization of one form under conditions on the other. For this result see Horn&Johnson, 1985, page 218 and following.
Negative-definite, semidefinite and indefinite matrices
The n × n Hermitian matrix M is said to be negative-definite if
for all non-zero 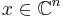 (or, all non-zero
(or, all non-zero 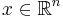 for the real matrix).
for the real matrix).
It is called positive-semidefinite (or sometimes nonnegative-definite) if
for all 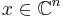 (or, all
(or, all 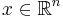 for the real matrix), where
for the real matrix), where 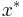 is the conjugate transpose of x.
is the conjugate transpose of x.
It is called negative-semidefinite if
for all 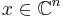 (or, all
(or, all 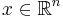 for the real matrix).
for the real matrix).
A matrix M is positive-semidefinite if and only if it arises as the Gram matrix of some set of vectors. In contrast to the positive-definite case, these vectors need not be linearly independent.
For any matrix A, the matrix A*A is positive semidefinite, and rank(A) = rank(A*A). Conversely, any Hermitian positive semidefinite matrix M can be written as M = A*A; this is the Cholesky decomposition.
A Hermitian matrix which is neither positive- nor negative-semidefinite is called indefinite.
A matrix is negative definite if all kth order leading principal minors are negative if k is odd and positive if k is even.
A Hermitian matrix is negative-definite, negative-semidefinite, or positive-semidefinite if and only if all of its eigenvalues are negative, non-positive, or non-negative, respectively.
Further properties
If M is an Hermitian positive-semidefinite matrix, one sometimes writes M ≥ 0 and if M is positive-definite one writes M > 0.[1] The notion comes from functional analysis where positive definite matrices define positive operators.
For arbitrary square matrices M,N we write M ≥ N if M − N ≥ 0; i.e., M − N is positive semi-definite. This defines a partial ordering on the set of all square matrices. One can similarly define a strict partial ordering M > N.
- Every positive definite matrix is invertible and its inverse is also positive definite.[2] If M ≥ N > 0 then N−1 ≥ M−1 > 0.[3]
- If M is positive definite and r > 0 is a real number, then r M is positive definite.[4] If M and N are positive definite, then the sum M + N[4] and the products MNM and NMN are also positive definite. If MN = NM, then MN is also positive definite.
- If M = (mij) ≥ 0 then the diagonal entries mii are real and non-negative. As a consequence the trace, tr(M) ≥ 0. Furthermore[5]
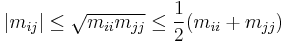
- and thus
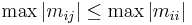
- If
 is a symmetric matrix of the form
is a symmetric matrix of the form 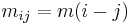 , and the strict inequality holds
, and the strict inequality holds
 is strictly positive definite.
is strictly positive definite. - A matrix M is positive semi-definite if and only if there is a positive semi-definite matrix B with B2 = M. This matrix B is unique,[6] is called the square root of M, and is denoted with B = M1/2 (the square root B is not to be confused with the matrix L in the Cholesky factorization M = LL*, which is also sometimes called the square root of M). If M > N > 0 then M1/2 > N1/2 > 0.
- If M,N > 0 then M ⊗ N > 0, where ⊗ denotes Kronecker product.
- For matrices M = (mij) and N = (nij), write M ° N for the entry-wise product of M and N; i.e., the matrix whose i,j entry is mijnij. Then M ° N is the Hadamard product of M and N. The Hadamard product of two positive-definite matrices is again positive-definite and the Hadamard product of two positive-semidefinite matrices is again positive-semidefinite (this result is often called the Schur product theorem).[7] Furthermore, if M and N are positive-semidefinite, then the following inequality, due to Oppenheim, holds:[8]
- Let M > 0 and N Hermitian. If MN + NM ≥ 0 (resp., MN + NM > 0) then N ≥ 0 (resp., N > 0).
- If M,N ≥ 0 are real positive semidefinite symmetric matrices, then
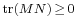 (Lancaster-Tismenetsky, The Theory of Matrices, p. 218).
(Lancaster-Tismenetsky, The Theory of Matrices, p. 218). - If M > 0 is real, then there is a δ > 0 such that M > δI, where I is the identity matrix.
Block matrices
A positive 2n × 2n matrix may also be defined by blocks:
Where each block is n × n. By applying the positivity condition, it immediately follows that A and D are hermitian, and C = B*.
We have that z*Mz ≥ 0 for all complex z, and in particular for z = ( v, 0)T. Then
A similar argument can be applied to D, and thus we conclude that both A and D must be positive definite matrices, as well.
Non-Hermitian matrices
A real matrix M may have the property that xTMx > 0 for all nonzero real vectors x without being symmetric. The matrix
satisfies this property, because for all real vectors 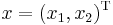 such that
such that 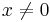 ,
,
In general, we have xTMx > 0 for all real nonzero vectors x if and only if the symmetric part, (M + MT) / 2, is positive definite.
The situation for complex matrices may be different, depending on how one generalizes the inequality z*Mz > 0 when considering M which aren't necessarily Hermitian. If z*Mz is real for all complex vectors z, then the matrix M must be Hermitian. To see this, we define the Hermitian matrices A=(M+M*)/2 and B=(M-M*)/(2i) so that M=A+iB. Then, z*Mz=z*Az+iz*Bz is real. By the Hermiticity of A and B, z*Az and z*Bz are individually real so z*Bz must be zero for all z. So then B is the zero matrix and M=A, which is Hermitian.
So, if we require that z*Mz be real and positive, then M is automatically Hermitian. On the other hand, we have that Re(z*Mz) > 0 for all complex nonzero vectors z if and only if the Hermitian part, (M + M*) / 2, is positive definite.
In summary, the distinguishing feature between the real and complex case is that, a bounded positive operator on a complex Hilbert space is necessarily Hermitian, or self adjoint. The general claim can be argued using the polarization identity. That is no longer true in the real case.
There is no agreement in the literature on the proper definition of positive-definite for non-Hermitian matrices.
See also
- Cholesky decomposition
- Positive-definite function
- Positive definite kernel
- Schur complement
- Square root of a matrix
- Sylvester's criterion
- Covariance matrix
Notes
- ^ This may be confusing, as sometimes nonnegative matrices are also denoted in this way. A common alternative notation is
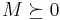 and
and 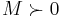 for positive semidefinite and positive definite matrices, respectively.
for positive semidefinite and positive definite matrices, respectively. - ^ Horn & Johnson (1985), p. 397
- ^ Horn & Johnson (1985), Corollary 7.7.4(a)
- ^ a b Horn & Johnson (1985), Observation 7.1.3
- ^ Horn & Johnson (1985), p. 398
- ^ Horn & Johnson (1985), Theorem 7.2.6 with k = 2
- ^ Horn & Johnson (1985), Theorem 7.5.3
- ^ Horn & Johnson (1985), Theorem 7.8.6
References
- Horn, Roger A.; Johnson, Charles R. (1985), Matrix Analysis, Cambridge University Press, ISBN 978-0-521-38632-6.
- Rajendra Bhatia. Positive definite matrices. Princeton Series in Applied Mathematics, 2007. ISBN 978-0691129181.
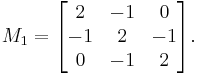
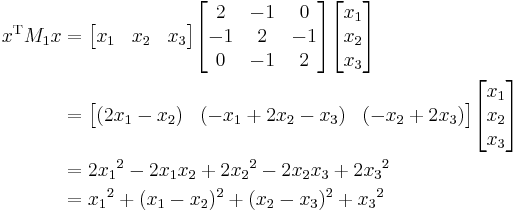
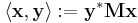
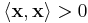 for all nonzero x.
for all nonzero x.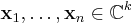
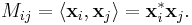
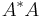 where A is not necessarily square but must be injective in general.
where A is not necessarily square but must be injective in general.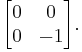
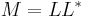 .
.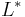 is the
is the 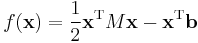
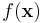 has a unique
has a unique